Modeling of the effect of lasers on energetic materials

The examination of the effect of intense laser radiation on energetic materials is of considerable importance for security and defense research. The application of high-power lasers offers, among others, great potential in the development of new procedures for the safe disarming of explosive devices, and in defense against mortar shells and rockets in military camps. The thereby occurring processes could not yet be adequately described so far and were recently experimentally and numerically compiled in a doctoral thesis.

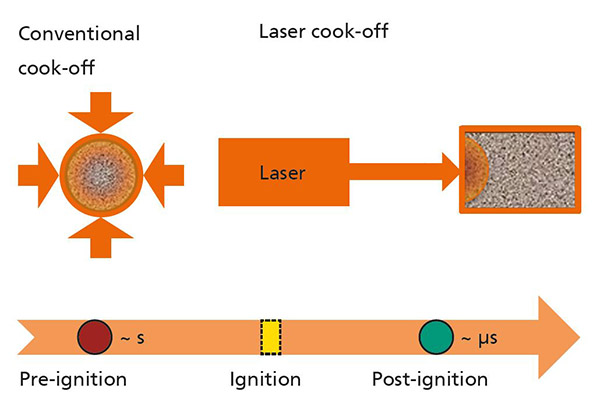
The laser cook-off

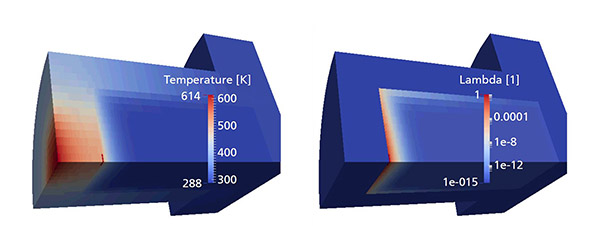
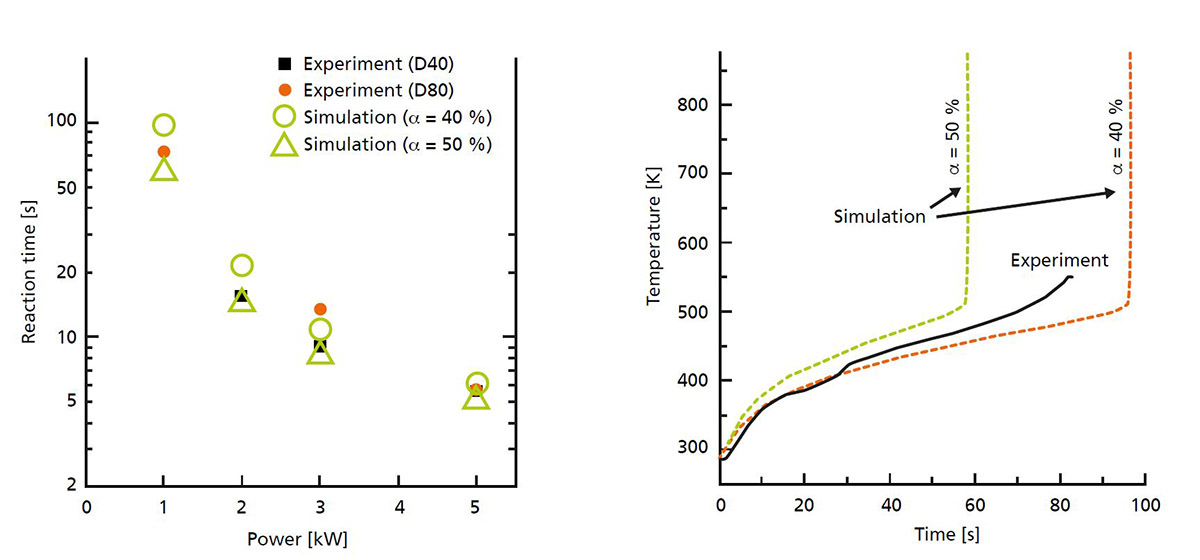
In order to assess the safety risk of explosive materials during a fire, certain cook-off tests are established, in which energetic materials are slowly heated until the point of thermal ignition (Figure 1). Analogously, the heating of energetic materials with a high-power laser is also considered a laser cook-off. In contrast to a conventional cook-off, the laser causes a local heating with a higher heating rate. This in turn entails a higher temperature gradient in the energetic material.

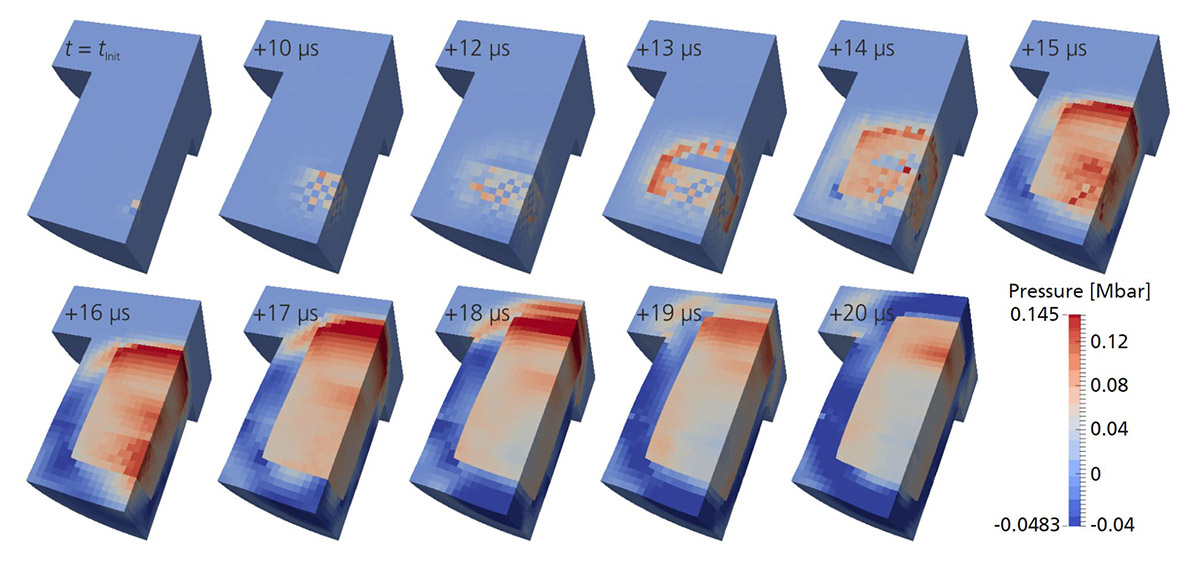
A cook-off begins with the pre-ignition phase (Figure 1), in which the energetic material is heated and an exothermic reaction begins and chemical energy is released. This reaction becomes self-sustaining the moment when more chemical energy is released than can be dissipated. This marks the time point of thermal ignition. The following post-ignition phase is characterized by the fast conversion of the still unspent energetic material. The quick release and expansion of gaseous reaction products characterizes the explosive mechanical impact of energetic materials. While it is of interest if and when an ignition occurs in the pre-ignition phase, in the post-ignition phase, the question of the reaction strength is in the focus.

Setup of a simulation environment

In order to gain a detailed understanding, a simulation environment was created in which the total reaction process including the heating-up phase and thermal initialization can be depicted. The modeling of relevant processes succeeded without additional assumptions but simply based upon physical principles and material parameters from scientific literature. The simulation environment was developed based upon an existing hydrocode, since hydrocodes are ideal for simulations of the highly dynamic post-ignition phase. The hydrocode was expanded to model not only the mechanical processes but also laser-induced energy coupling and thermal or chemical processes.

A particular challenge arose due to the vastly different time scales of the individual processes. The ignition time point when using a laser at the lowest power of one kilowatt was at approximately one minute. The simulation of such a long process in an explicitly integrated hydrocode would take too long due to the small, yet critical mechanical time step of in the order of one microsecond. For that reason, a multi-time-scale approach was developed in which the mechanical processes could be disregarded and instead, the larger time step of the heat conduction is used –in this case, approximately 100,000 times larger. Figure 3 shows the two stability criteria for steel as a function of the element size. If the mechanical processes in the post-ignition phase, or rather shortly before ignition, are taken into consideration, the multi-time-scale approach will allow for a time step reduction (see Figure 4). As soon as the time step lies under the value of the mechanical stability criterion, the energy balance, mass balance, and impulse balance can be solved.

Simulation of the pre-ignition phase

The first step was to model the pre-ignition phase, taking thermal and chemical processes into consideration while disregarding mechanical processes. The simulation includes the coupling of laser beam onto the steel casing, the heat conduction through the steel casing and into the energetic material, and its chemical reaction per a reaction law of Arrhenius kinetics. A procedure for temperature calculation was developed and validated for this case, which allows for the consideration of a temperature-dependent specific heat capacity for the hydrocode-typical explicit temporal integration procedure.

The cylindrical specimens that were irradiated in the experiment were three-dimensionally modeled with quarter-symmetry in the simulation. Figure 5 depicts the simulated distribution of the temperature and the reaction process “Lambda”, l, at the moment of initialization of a laser power of one kilowatt. The simulation environment was validated by the experimental measurement data. In Figure 6, the right graph depicts experimental and simulated temperature curves for a laser power of one kilowatt, while on the left, resulting reaction times for a laser power of up to five kilowatts are illustrated. Within the expected absorbance, the accordance of the experimental values with the simulation results is very good.

Thermal-chemical-mechanical simulation of the entire laser cook-off

An important alteration in the modeling approach is the possibility to simulate mechanic processes and, thereby, the post-ignition phase. A model for the energetic material was implemented in addition to the above described multi-time-scale approach. This model can depict the simultaneous occurrence of solid reactants and gaseous products during the chemical reaction with a rule of mixture in a numerical element. Accordingly, the specific volumes and specific internal energies of the two phases (solid_s, gas_g) weighted by the progress of the reaction add up to the volume or energy of the entire element. It is assumed that both phases are in thermal and mechanical balance, which means their pressure and temperature are the same. The phase pressures and temperatures were described with thermal, or caloric, equations of state. The material model is iteratively solved.

The calculation of the above described material models is computationally intensive. For the typical high temperature gradient present in a laser cook-off, a delicate interlacing in the energetic material is required to be able to reliably predict the experimental test period. This in turn results in impractically high computing times. In order to obtain a sufficiently exact result, even with a less fine interlacing, a temperature interpolation approach was developed for the reaction law. As opposed to a constant temperature, a section-by-section linear temperature distribution in an element is assumed, inserted into the Arrhenius law, and then integrated via the element volume. The convergence of this procedure could be proven by numerical analyses, even for less fine resolutions. Thereby, a complete, exact and computationally efficient laser cook-off simulation, from the pre-ignition phase to the ignition to the post-ignition phase, is possible.

To demonstrate the potential of this procedure, Figure 7 depicts the simulation of the processes in the post-ignition phase, in which the conversion of the explosive material following the ignition can be calculated using a known, pressure-dependent reaction model. The development of a detonation wave after the thermal initialization and an additional induction time can also be modeled for the laser cook-off. Based upon the ability of the simulation environment, future works could, among other things, coordinate the modeling of a reaction in the post-ignition phase with experimental results even better, including non-detonating conversions.